عدد طلايي

پاره خطي را در نظر بگيريد و فرض کنيد که آنرا بگونه اي تقسيم کنيد که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنيد. اگر اين معادله ساده يعني a2=a*b b2 را حل کنيم (کافي است بجاي b عدد يک قرار دهيم بعد a را بدست آوريم) به نسبتي معادل تقريبا" 1.61803399 يا 1.618 خواهيم رسيد.
شايد باور نکنيد اما بسياري از طراحان و معماران بزرگ براي طراحي محصولات خود امروز از اين نسبت طلايي استفاده مي کنند. چرا که بنظر ميرسد ذهن انسان با اين نسبت انس دارد و راحت تر آنرا مي پذيرد. اين نسبت نه تنها توسط معماران و مهندسان براي طراحي استفاده مي شود بلکه در طبيعت نيز کاربردهاي بسياري دارد که به تدريج راجع به آن صحبت خواهيم کرد.

يک بناي يونان باستان که نسبت طلايي در ساختار آن مشاهده مي شود.

مثلث قائم الزاويه اي که با نسبت هاي اين هرم شکل گرفته شده باشد به مثلث قائم مصري يا Egyptian Triangle معروف هست و جالب اينجاست که بدانيد نسبت وتر به ضلع هم کف هرم معادل با نسبت طلايي يعني دقيقا" 1.61804 مي باشد. اين نسبت با عدد طلايي تنها در رقم پنجم اعشار اختلاف دارد يعني چيزي حدود يک صد هزارم. باز توجه شما را به اين نکته جلب مي کنيم که اگر معادله فيثاغورث را براي اين مثلث قائم الزاويه بنويسم به معادله اي مانند phi2=phi b2 خواهيم رسيد که حاصل جواب آن همان عدد معروف طلايي خواهد بود. (معمولا" عدد طلايي را با phi نمايش مي دهند)
طول وتر براي هرم واقعي حدود 356 متر و طول ضلع مربع قاعده حدودا" معادل 440 متر مي باشد بنابر اين نسبت 356 بر 220 (معادل نيم ضلع مربع) برابر با عدد 1.618 خواهد شد.
کپلر (Johannes Kepler 1571-1630) منجم معروف نيز علاقه بسياري به نسبت طلايي داشت بگونه اي که در يکي از کتابهاي خود اينگونه نوشت : "هندسه داراي دو گنج بسيار با اهميت مي باشد که يکي از آنها قضيه فيثاغورث و دومي رابطه تقسيم يک پاره خط با نسبت طلايي مي باشد. اولين گنج را مي توان به طلا و دومي را به جواهر تشبيه کرد".
تحقيقاتي که کپلر راجع به مثلثي که اضلاع آن به نسبت اضلاع مثلث مصري باشد به حدي بود که امروزه اين مثلث به مثلث کپلر نيز معروف مي باشد. کپلر پي به روابط بسيار زيبايي ميان اجرام آسماني و اين نسبت طلايي پيدا کرد. براي اطلاع بيشتر از نحوه محاسبه نسبت طلايي به اين سايت سري بزنيد.
0,1,1,2,3,5,8,13,21,34,55,89,144, ...

البته برخي از رياضي دانان عدد صفر را جزو رشته فيبوناچي نمي دانند و يا حداقل آنرا جمله صفرم سري مي دانند. نکته اي که تعجب برانگيز است آنکه اگر از عدد سوم نسبت اعداد اين سري را به عدد قبلي حساب کنيم خواهيم داشت :
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
و يا :
1, 2, 1.5, 1,666, 1.6, 1,625, 1.6153, 1.6190, 1.6176, 1.6181, 1.6179و ...
بله بنظر مي رسد که اين رشته به سمت همان عدد طلايي معروف ميل ميکند. بگونه اي که اگر نرخ عدد چهلم اين رشته را به عدد قبلي حساب کنيم به عدد 1.618033988749895 مي رسيم که با تقريب 14 رقم اعشار نسبت طلايي را نشان مي دهد.
بعدها محاسبات و استدلال هاي رياضي نشان داد که اين سري همگرا به سمت نسبت طلايي مي باشد و جمله عمومي آنرا با بتقريب مي توان اينگونه نمايش داد :
fn = Phi n / 5½
که در آن Phi عدد طلايي ميباشد. البته فرمول هاي دقيق ديگري وجود دارند که اعداد سري و يا اعداد بعدي (Successor) اين سري را نمايش مي دهند که دراين مطلب به آن نخواهيم پرداخت.
معماي زاد و ولد خرگوش!
در واقع فيبوناچي در سال 1202 به مسئله عجيبي علاقمند شد. او مي خواست بداند اگر يک جفت خرگوش نر و ماده داشته باشد و رفتاري براي زاد و ولد آنها تعريف کند در نهايت نتيجه چگونه خواهد شد. فرضيات اينگونه بود :
- شما يک جفت خرگوش نر و ماده داريد که همين الآن بدنيا آمده اند.
- خرگوشها پس از يک ماه بالغ مي شوند.
- دوران بارداري خرگوشها يک ماه است.
- هنگامي که خرگوش ماده به سن بلوغ مي رسد حتما" باردار مي شود.
- در هر بار بارداري خرگوش ماده يک خرگوش نر و يک ماده بدنيا مي آورد.
- خرگوش ها هرگز نمي ميرند.
حال سئوال اينجاست که پس از گذشت يکسال چه تعداد خرگوش نر و چه تعداد خرگوش ماده خواهيم داشت؟ (پاسخ را شما بدهيد)
به شکل زير نگاه کنيد و ببينيد که به چه زيبايي از کنار هم قرار دادن تعدادي مربع مي توان رشته فيبو ناچي را بصورت هندسي نمايش داد. حال اگر در هر يک از اين مربع ها از نقاط قرمز ربع دايره هايي رسم کنيم در نهايب به نوعي از مارپيچ حلزوني شکل مي رسيم که به مارپيچ فيبوناچي (Fibonacci Spiral) معروف مي باشد. بديهي است که نرخ رشد و باز شدن اين مارپيچ متناسب با نرخ بزرگ شدن اعداد در سري فيبوناچي مي باشد.


سري فيبوناچي چه در رياضيات چه در فيزک و علوم طبيعي کاربردهاي بسيار ديگري دارد، ارتباط زيباي فاصله هاي خوش صدا در موسيقي، چگونگي تولد يک کهکشان و ... که کاربرد اين سري جادويي را بيش از پيش نشان مي دهد.
طريقه رسم نسبت طلايي با گونيا و پرگار
پاره خط AB را در نظر بگيريد. مساله ما يافتن نقطه E بر روي اين پاره خط مي باشد به طوري که نسبت AE به EB يک نسبت طلايي باشد.
مرحله 1 : از نقطه B خط BC را عمود بر آن طوري رسم کنيد که اندازه BC نصف اندازه AB باشد. ( به کمک پرگار مي توانيد اين کار را انجام بدهيد.)
مرحله 2 : نقطه A را به نقطه C وصل کنيد.
مرحله 3 : از نقطه C دايره اي به شعاع BC رسم کنيد. اين دايره خط AC را در نقطه D قطع مي کند.
مرحله 4 : از نقطه A يک دايره به شعاع AD رسم کنيد. اين دايره خط AB را در نقطه E قطع مي کند به قوري که نسبت AE به EB همان نسبت طلايي است.

طريقه رسم مستطيل طلايي با گونيا و پرگار
مستطيل CBGD را در نظر بگيريد. مساله ما يافتن مستطيلي است که نسبت اضلاع آن يک نسبت طلايي باشد.
مرحله 1 : نقطه A را در وسط DG پيدا کنيد.
مرحله 2 : از نقطه A يک دايره به شعاع AB رسم کنيد.
مرحله 3 : خط DG را ادامه داده تا دايره به مرکز A را در نقطه E قطع کند. نسبت DE به DC همان نسبت طلايي است و مستطيل CFED يک مستطيل طلايي مي باشد.

نسبت طلايي در خوشنويسي
استاد ميرعماد با پالايش خطوط پيشينيان و زدودن اضافات و ناخالصيها از پيکره نستعليق و نزديک کردن شگرف نسبتهاي اجزاي حروف و کلمات، به اعلا درجه زيبايي يعني نسبت طلايي رسيد و قدمي اساسي در اعتلاي هنر نستعليق برداشت. با بررسي اکثريت قاطع حروف و کلمات ميرعماد متوجه ميشويم که اين نسبت به عنوان يک الگو در تار و پود حروف و واژهها وجود دارد و زاويه 448/63 درجه که مبناي ترسيم مستطيل طلايي است، در شروع قلم گذاري و ادامه رانش قلم، حضوري تعيين کننده دارد. اين مهم قطعاً در سايه شعور و حس زيباييشناسي وي حاصل آمده، نه آگاهي از فرمول تقسيم طلايي از ديدگاه هندسي و علوم رياضي. ميرعماد اين نسبتها را نه تنها در اجزاي حروف بلکه در فاصله دو سطر و مجموعه دو سطر چليپاها و کادرهاي کتابت و قطعات رعايت ميکرده است.

نسبت طلايي در طبيعت
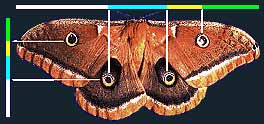
به اشکال شبيه چشم روي بدن پروانه که علامت گذاري شده است،توجه کنيد.نسبت فواصل طولي و عرضي اين علائم يک نسبت طلائي است.
پوسته مارپيچي يک حلزون نمونه اي ساده ودرعين حال زيبا، از نسبت طلائي است.

نسبت طلايي در ساقه گياهان

نسبت طلايي در عکاسي
ترکيب بندي تصوير، در کتابها و مجلات تخصصي عکاسي، اغلب به شکل يک نسخه تجويزي ارائه ميشود. انگار که پيروي از تعدادي قاعده ميتواند نتيجه قانع کننده اي را تضمين کند. شايد بهتر باشد اين قواعد را تنها به عنوان چکيده ايده هايي در نظر گرفت که عکاسان (و البته نقاشان و ساير هنرمندان قرنها پيش از اختراع دوربين) آنها را براي خلق يک تصوير تاثير گذار، مفيد يافته اند.
هر ترکيب بندي عکسي را ميتوان کارآمد دانست به شرط اين که عناصر صحنه به طور موثر با بينندگان مورد نظر آن عکس، ارتباط برقرار کند. در اغلب موارد، نکته اساسي در شناسايي عناصر کليدي صحنه نهفته است تا با تنظيم محل دوربين و ميزان نور دهي، آنها را از دل ساير اطلاعات تصويري متفرقه، بيرون بکشيد. همين اشياء مزاحم، بسياري از عکسها را خراب ميکنند. اگر عکاسي را تازه شروع کرده ايد، بهتر است به جاي تمرکز زياد روي جزييات خيلي خاص، تنها روي ساختار کلي صحنه تمرکز کنيد. چرا که تاثير آنها در مقابل ترکيب بندي عمومي عکس، بسيار سطحي است.
در اين مقاله به معرفي سه روش کاربردي در امر ترکيب بندي تصوير پرداخته خواهد شد. در آغاز به معرفي کلي تکنيکي ميپردازيم که قرنهاست شناخته شده است يعني قانون تعادل (يا قانون طلايي - Golden Mean). اين قانون در واقع يک فرمول هندسي است که توسط يوناني هاي باستان ابدا شده.استدلال بر اين است که ترکيب بندي اي که بر اساس اين تئوري تشکيل شده باشد، تاثيرگذار و قوي مينمايد. ايده اصلي که در پس اين تئوري است در واقع استفاده از خطوط هندسي است که به سادگي توسط چشم بيننده دنبال شوند. طي قرون متمادي، قانون تعادل (يا قانون طلايي - Golden Mean) راهبردي مهم و ابزاري کارآمد براي هنرمندان و نقاشان به حساب مي آمد. امروزه با توجه به ارزش اين ابزار، آشنايي با آن به عکاسان نيز توصيه ميشود.
قانون يک سوم (خطوط و نقاط طلايي):
قانون يک سوم در واقع مختصر شده مفهوم طلايي است. فلسفه اصلي که در پشت اين مفهوم قرار دارد از يک ترکيب و کادر بندي متقارن و مستقر در مرکز کادر که معمولا کسل کننده است جلوگيري مي کند. 4 خط تقسيم کننده کادر، خطوط طلايي و محل برخورد اين خطوط، نقاط طلايي ناميده ميشوند. (شکل هاي شماره يک و دو)
از بين بردن تقارن با استفاده از قانون يک سوم به دو شکل مي تواند صورت بگيرد. در يک روش مي توان تصوير را به دو بخش مجزا تقسيم کرد به نحوي که يک قسمت يک سوم و قسمت ديگري دو سوم تصوير را شامل شود (شکل شماره يک).
| شکل شماره يک |
|
|
در روشي ديگر، تمرکز مستقيما بر روي نقاط طلايي است. فرض کنيد که منظره اي بسيار زيبا و بديع پيش رو داريد اما اين منظره فاقد يک نماي هندسي و به اصطلاح Geometric خوب و جذاب است. به عبارت ديگر در عين اينکه منظره بسيار خاص و زيبا است اما اگر به صورت تصوير در بيايد تا حدودي کسل کننده خواهد شد.
راه حل چيست؟ سعي کنيد در اين منظره يکنواخت يک نقطه عطف و تمايز پيدا کنيد، نقطه اي که بتواند يکنواختي و يکدستي نما را از بين ببرد. سپس اين سوژه را روي يکي از نقاط طلايي قرار دهيد. اين نقطه اولين نگاه بيننده را جذب کرده و مخاطب را به ديدن باقي تصوير دعوت ميکند. (شکل شماره دو)
| شکل شماره دو |
|
|
براي تعيين برخي از اندازه ها به نسبتهاي شکيل و زيبا، معروفترين فرمول، شيوه اي است که يونانيان باستان ابداع کرده اند و به " نسبت طلايي" معروف است . نسبت طلايي در اصل، فرمولي رياضي و داراي زيبايي بصري است. در اين روش : ابتدا مربع را با خطي عمود بر دو ضلع مربع به دو مستطيل مساوي تقسيم مي کنند، سپس محل تقاطع آن خط با يکي از اضلاع مربع ( نقطه X) را مرکز دايره اي به شعاع قطر مستطيل قرار مي دهند ( فاصله X تا Y) و با ترسيم اين دايره و تعيين محل تقاطع آن با امتداد ضلع مربع ( نقطه Z) طول مستطيلي معروف به "مستطيل طلايي" به دست مي آيد که عرض آن برابر ضلع مربع و است و نسبت اين طول و عرض ثابت و داراي زيبايي خاصي است (نسبت اندازه پاره خط C به A با نسبت اندازه A به B يکي است) يونانيان در ساخت بسياري از اشيا و ابينه و معابد و کوره ها و ... آن را به کار مي بستند.

قانون يک سوم کادر نيز در واقع همان مفهوم طلايي است. 4 خط تقسيم کننده يک کادر، خطوط طلايي و محل برخورد اين خطوط، نقاط طلايي ناميده ميشوند.
مارپيچ طلايي
يکي از ابزارهاي ترکيب بندي عکس براي هدايت چشم بيننده به نقطه مورد نظر عکاس، مارپيچ طلايي است. استفاده از اين تکنيک در سوژه هايي که با نقاط طلايي سازگار نبوده اند قابل استفاده است. نحوه رسم مارپيچ طلايي نيز به اين صورت است.


 |
در بدن انسان مثالهاي بسيار فراواني از اين نسبت طلايي وجود دارد. در شکل زير نسبت M/m يک نسبت طلايي است که در جاي جاي بدن انسان مي توان آنرا ديد. به عنوان مثال نقاطي از بدن که داراي نسبت طلايي هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج
نسبت فاصله شانه تا بالاي سر به اندازه سر
نسبت فاصله ناف تا بالاي سر به فاصله شانه تا بالاي سر
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا
اينها تنها چند مثال از وجود نسبت طلايي در بدن انسان بود که بدن انسان را در حد کمال زيبايي خود نشان مي دهد.


در تصاوير زير نسبت خط سفيد به آبي، آبي به زرد، زرد به سبز و سبز به بنفش يک نسبت طلايي است!!




